
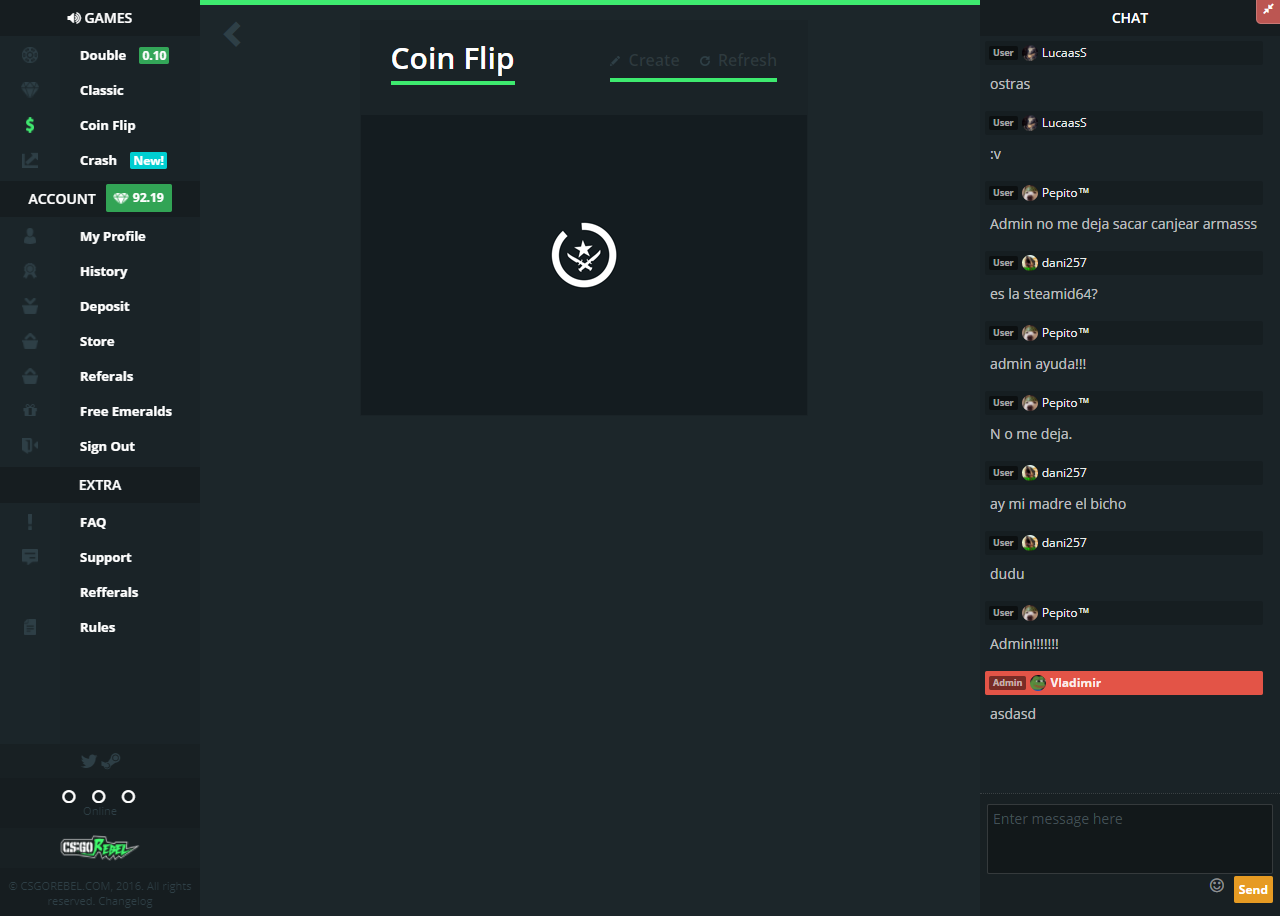
The machine completes a flip approximately every two seconds, meaning 10,000 flips would take approximately 2.5 days. Once the flip has been analysed, a sliding aperture is used to push the coin back towards the flipper for the next cycle.

A black spot is used on one side of the coin to aid analysis, as the poor-quality webcam images weren’t good enough to recognise the coin in its standard form. An image processing pipeline then determines whether the coin landed heads or tails.

Once the coin has landed, it is photographed with a webcam. A spring-loaded dowel is actuated by a stepper motor spinning a cam, which flips the coin. A large cylindrical shroud is used to keep the coin within the flipping area. The build consists largely of 3D printed parts. Of course, if you want to test this, it pays to have a machine do the hard work for you. Often, there is talk of how, given a fair coin, the probability of landing heads or tails should approach 0.5. The game is over, and Bob has won.Flipping a coin is often the initial example used to help teach probability and statistics to maths students. He does this, and he says to Alice "you lose, here are your factors". If Alice communicated the number $x'$ or $n-x'$, Bob can use this information and the fact that he knows the other square root, namely $x$, to find the factors of $n$. Then Alice reads the factors $p$ and $q$ to him over the phone, and Bob can check that they are both prime numbers and that $n = pq$. If Alice communicated the number $x$ or $n-x$, he says to Alice "you win, but you must now tell me the factors $p$ and $q$". Alice chooses one of these square roots and reads it to Bob over the phone.īob compares the number read to him over the phone to the number that he chose. Alice can compute them all, but she does not know which number Bob has chosen. There are four such square roots, let's say $x$ and $n-x$ and $x'$ and $n-x'$. Since Alice knows the factorization of n, she can compute the square roots of $a$ modulo $n$. He computes the square $a = x^2 \mod n$ and reads it to Alice over the phone. She keeps the numbers $p$ and $q$ secret.īob chooses a random integer $x$ between $1$ and $n$. She computes the number $n = pq$ and reads it to Bob over the phone. This was answered by Manuel Blum in 1983.īlum proposed a scheme that is similar in security to RSA.Įdit: Here is a summary of Blum's approach.Īlice chooses two large prime numbers $p$ and $q$, with the property $p \equiv 3 \mod 4$ and $q \equiv 3 \mod 4$. The point of $r_B$ is so that, without it, Alice might pick some $r_A$ for which she knows another string $r$ which might let her lie. Essentially, the purpose of $r_A$ and $h$ are to make Alice "commit" to her initial toss $x$. Moreover, it's extremely hard for Alice to cheat because if Bob says "tails" for example when the coin toss was indeed "tails" but Alice wants to trick him into thinking it was "heads", she'd have to come up with a random string $r$ such that $h(H,r,r_B) = h(T,r_A,r_B)$, which is hard by the assumption that $h$ is a secure hash function and the fact that Bob chose $r_B$. Obviously, if Bob calls the coin flip correctly, then the two hashes match. In this way if Bob called it wrong, then Alice can prove that he was wrong. Then Alice tells Bob $(x,r_A)$ and he can verify himself that $x = y$ by checking that $h(x,r_A,r_B) = h(y,r_A,r_B)$. Alice sends $h(x,r_A,r_B)$ to Bob and asks Bob to call the toss. Now, Alice flips a coin, call the result $x$. Alice chooses a random string $r_A$ and Bob chooses a random string $r_B$. Let's call the two parties Alice and Bob (as is popular to do in cryptography and theoretical computer science more broadly these days).Īlice and Bob agree on a secure hash function $h$.


 0 kommentar(er)
0 kommentar(er)
